Цилиндрические винтовые линии
По этой ссылке вы найдёте полный курс лекций по математике:
Цилиндрическая винтовая линия представляет собой пространственную кривую линию одинакового уклона. Острие резца, соприкасаясь с поверхностью равномерно вращающегося цилиндрического стержня, оставляет на нем след в виде окружности. Если же при этом сообщить резцу равномерное поступательное движение вдоль оси цилиндра, то на поверхности цилиндра получится цилиндрическая винтовая линия.
На рисунке 218 показано образование винтовой линии на поверхности цилиндра от движения точки А по образующей ЕС и вращательного движения этой образующей. Здесь изображено несколько положений этой образующей: £0С0, £,С„ . ; при этом дуги £,£,, . равны между собой и каждая равна nd/n, где d — диаметр цилиндра, а п — число делений (на рисунке 218 п= 12). Начальное положение точки обозначено через Д), последующее через Л,, Л, и т. д.
Если при перемещении образующей из положения £0С0 в положение £,С, точка займет положение А>, то отрезок £,/1, определит расстояние, которое точка прошла по образующей от своего первоначального положения. При последующем положении образующей (£>С) точка поднимется на высоту Е2А2-2Е[А[ и т. д. Когда образующая сделает полный оборот, точка переместится по ней на расстояние ЕсАа = 12£,/1,. При дальнейшем вращении образующей точка А начнет образовывать второй виток, или оборот винтовой линии, занимая положения А\, А\ и т. д.
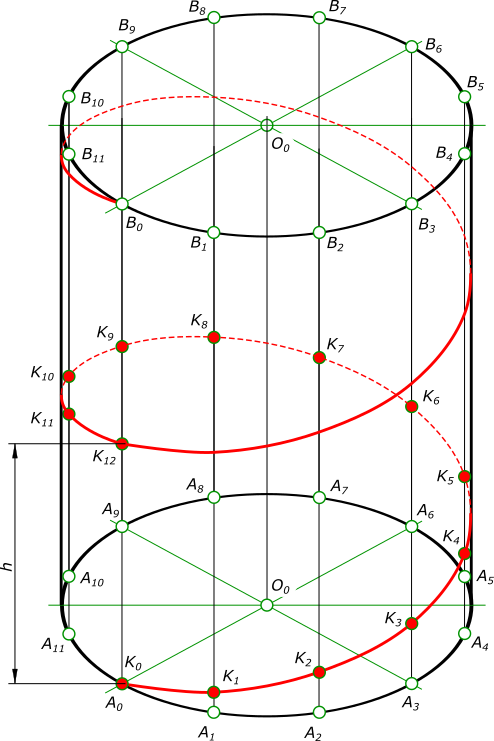
На рисунке 219 выполнено построение проекций цилиндрической винтовой линии. Предварительно построены проекции (как это рассматривалось в курсе черчения средней школы) прямого кругового цилиндра. Окружность основания цилиндра (на горизонтальной проекции) и шаг (отрезок h, отложенный по оси цилиндра на фронтальной проекции) разделены на одинаковое число (п) частей; на рисунке 219 взято п- 12. Начальное положение точки А указано проекциями А» и А’ — это точка, отмеченная буквой О’ на окружности.
Так как ось цилиндра направлена перпендикулярно к плоскости ли то горизонтальная проекция винтовой линии сливается с окружностью, представляющей собой горизонтальную проекцию поверхности цилиндра.
Возможно вам будут полезны данные страницы:
Что же касается построения фронтальной проекции винтовой линии, то ход ее построения ясен из рисунка 219 и вытекает из самого образования винтовой линии как траектории точки, совершающей лва движения — равномерное по прямой линии и вместе с тем равномерное вращательное вокруг оси, параллельной этой прямой. Проекция на плоскости, параллельной оси цилиндра, в данном случае фронтальная проекция цилиндрической винтовой линии, подобна синусоиде.
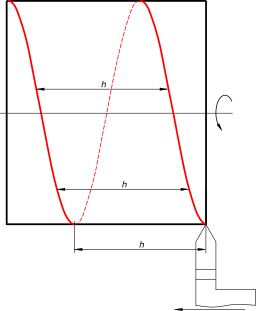
На рисунке 219 фронтальная проекция винтовой линии имеет на передней (видимой) стороне цилиндра подъем слева направо или спуск влево; если же ось цилиндра расположить горизонтально, то подъем винтовой линии идет влево, а спуск — вправо. Это винтовая линия с правым ходом, или правая винтовая линия. Развертка витка цилиндрической винтовой линии показана на рисунке 220. В развернутом виде каждый виток представляет собой отрезок прямой.
Это следует из образования винтовой линии: поскольку окружность основания цилиндра делилась на равное число частей и шаг винтовой линии делился на такое же число равных частей, развертку винтовой линии на протяжении ее шага можно рассматривать как геометрическое место точек, для каждой из которых ордината пропорциональна абсциссе, т. е. у= кх. А это уравнение прямой линии. Касательные к винтовой линии совпадают на развертке с прямой, в которую развертывается виток винтовой линии.
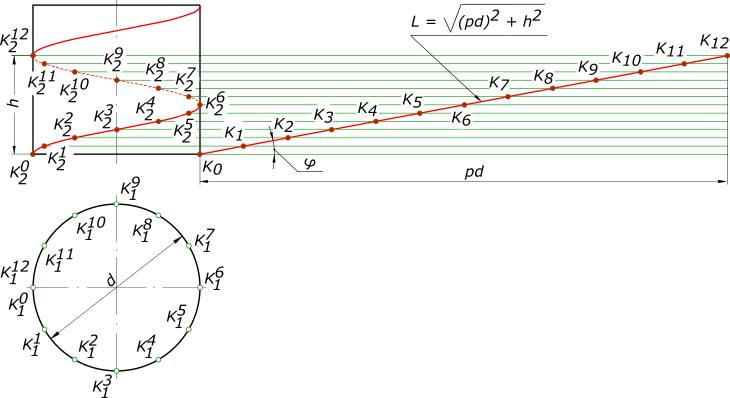
| На рисунке 220 при двух шагах |
винтовой линии получились два ее отрезка под углом ф, к прямой, представляющей собой развернутую окружность основания цилиндра. Крутизна подъема винтовой линии выражается формулой (2): tg«>i=4> (2) ГШ где h — шаг винтовой линии; d — диаметр цилиндра. Угол ф, называется углом подъема винтовой линии. _
Длина одного оборота «витка» винтовой линии равна L = + (nd)2. При одном и том же d величина угла ф, зависит только от шага винтовой линии; для получения малого угла подъема следует брать малый шаг, и наоборот. Если шаг остается неизменным для цилиндров разного диаметра, то угол подъема получится тем меньше, чем больше будет диаметр цилиндра. Вопросы для самопроверки 1. В чем состоит различие между плоской и пространственной кривыми линиями?
2. Во что проецируется пространственная кривая? 3. Во что проецируется плоская кривая? 4. Во что проецируется касательная к кривой линии? 5. Как определяется длина некоторого участка кривой линии? 6. Что называется касательной к кривой линии? 7. Что называется нормалью в какой-либо точке плоской кривой? 8. Что называется шагом винтовой линии? 9. Что такое правая винтовая линия? 10. Как определяется крутизна подъема винтовой линии? 11. Какие параметры определяют цилиндрическую винтовую линию?
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник
Винтовая линия
Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии.
Цилиндрическая винтовая линия описывается точкой, которая совершает равномерное движение вдоль образующей кругового цилиндра, а образующая вращается с постоянной угловой скоростью вокруг оси цилиндра.
Образующая занимает 12 последовательных положений: A 0 B 0 . Дуги A 0 A 1 , A 1 A 2 A 2 A 3 и т. д. равны между собой и каждая равна pd/n, где d — диаметр цилиндра, p = 3,14 и n — число положений образующей цилиндра, принятое для построения. Пусть образующая занимает 12 последовательных положений: A 0 B 0 , A 1 B 1 , A 2 B 2 и т. д. Начальному положению образующей AB соответствует A 0 B 0 , а точки K — K 0 . При перемещении образующей AB в положение A 1 B 1 точка K займет положение K 1 , и поднимется по образующей на величину отрезка A 1 K 1 = h/12. При последующем перемещении образующая займет положение A 2 B 2 , а точка K положение K 2 и поднимется на высоту равную A 2 B 2 = 2A 1 B 1 = 2(h/12), и т. д. Когда образующая совершит полный оборот и снова займет начальное положение, точка K будет находится на ней на высоте A 12 B 12 = 12(h/12) = h, величине шага винтовой линии. При этом точка описывает кривую K 0 K 6 K 12 , длина которой равна длине одного витка. На практике эти движения достигаются на токарном станке, где острие резца соответствует данной точке.
Резец оставит на цилиндрической поверхности след — винтовую линию. Винтовая линия может быть правой или левой. Правой винтовой линией называют линию, совершающую подъем вокруг своей оси против часовой стрелки, а левой — винтовую линию, совершающую подъем по часовой стрелке. Правая цилиндрическая винтовая линия
может быть построена, когда заданы ее элементы. Винтовая линия характеризуется следующими элементами: шаг, виток и угол подъема. Шагом винтовой линии называется расстояние между смежными витками, измеренное вдоль образующей кругового цилиндра. Витком называют винтовую линию, описанную точкой за один оборот образующей вокруг оси кругового цилиндра. Длина витка равна L. Углом подъема винтовой линии называют отношение tg(φ)= h/(pd), тогда φ = arctg(φ), где d — диаметр цилиндра, p=3,14.
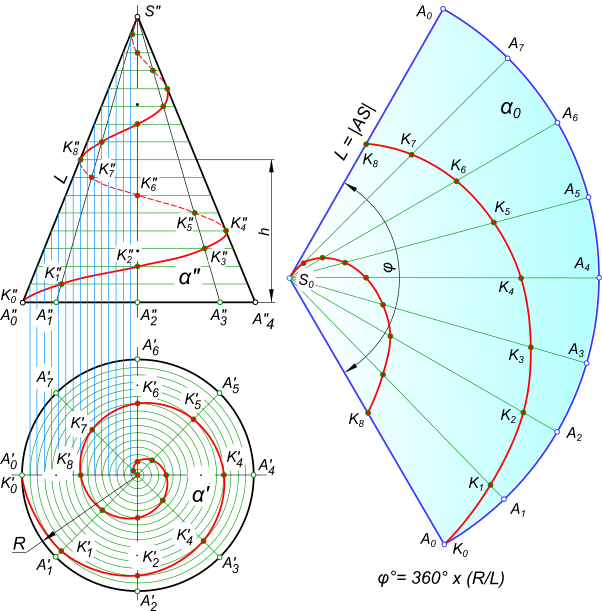
Винтовая линия может быть получена на конической поверхности
В этом случае, точка совершает равномерно-поступательное движение вдоль образующей прямого кругового конуса, а сама образующая SA вращается вокруг его оси с постоянной угловой скорости. Расстояние между точками смежных витков, измеренное параллельно оси конуса (например между точками A0K8), является шагом h конической винтовой линии. Проекция винтовой линии на фронтальной плоскости проекций представляет собой синусоиду с затухающим колебанием (затухающей волной), а на горизонтальной — спираль Архимеда. При построении развертки боковой поверхности конуса винтовая линия развернется в спираль, а конус — в сектор, угол при вершине которого равен φ= 360°×(h/L), а длина дуги радиуса R, соответствующая углу φ, равна 2πR.
Источник
Физика дома
Задача на определение шага винтовой линии при движении частицы в магнитном поле может быть полезна всем, кто сдаёт физику.
Частица, несущая заряд электрона и имеющая импульс 10 -23 кг*м/с, влетает в однородное магнитное поле с индукцией 0,01 Тл под углом 60 0 к линиям индукции. Определите шаг винтовой линии, вдоль которой будет двигаться частица.
Для начала, как обычно, нужно сделать рисунок и изобразить траекторию движения заряженной частицы.
На частицу в магнитном поле действует сила Лоренца, которая сообщает ей центростремительное ускорение. Но поскольку вектор скорости образует некоторый угол с направлением вектора магнитной индукции, частица будет перемещаться вдоль этой линии по спирали. Шаг этой спирали (винтовой линии) мы должны будем определить.
За радиус винтовой линии отвечает игрековая составляющая вектора скорости, а за перемещение вдоль вектора магнитной индукции — иксовая составляющая вектора скорости. (В отсутствии электрического поля частица будет двигаться равномерно с постоянным шагом).
Шаг винтовой линии — это то расстояние, которое пролетает заряженная частица за время, равное периоду обращения. И одна из задач будет доказать, что период обращения частицы не зависит от скорости, а следовательно, и от угла ( формула периода обращения частицы в магнитном поле не является обязательной для запоминания).
Умножая проекцию скорости на ось, совпадающую с направлением вектора магнитной индукции, на период (время движения частицы по одному звену спирали), получаем итоговую формулу для шага винтовой линии. Остаётся подставить численные значения известных физических величин и определить числовое значение шага винтовой линии (спирали).
Источник
Учебники
Журнал «Квант»
Общие
§14. Движение заряженных частиц в электрическом и магнитном полях
14.3 Движение по винтовой линии в однородном магнитном поле.
Рассмотрим теперь произвольный случай движения заряженной частицы в однородном магнитном поле.
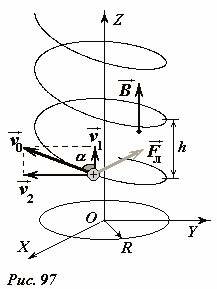
Введем систему декартовых координат, так, чтобы вектор индукции однородного магнитного поля \(
\vec B\) был направлен вдоль оси Oz (рис. 97). Пусть вектор скорости \(
\vec \upsilon_0\) частицы массы m, имеющей электрический заряд q, направлен под произвольным углом α к вектору индукции поля. Разложим этот вектор на две составляющих\[
\vec \upsilon_1\] — параллельную вектору индукции и \(
\vec \upsilon_2\) — перпендикулярную ему. Действующая на частицу сила Лоренца \(
\vec F_L\) перпендикулярна векторам скорости и индукции, то есть лежит в плоскости xOy. Модуль этой силы равен
F_L = q \upsilon_0 B \sin \alpha = q \upsilon_2 B\) . (1)
Если спроецировать уравнение второго закона Ньютона для частицы
m \vec a = q \vec \upsilon \times \vec B\) , (2)
на плоскость xOy, то получим уравнение, в которое только компонента скорости, перпендикулярная полю. Это уравнение описывает движение частицы, движущейся перпендикулярно вектору индукции, которое было подробно рассмотрено ранее. Оно представляет собой равномерное движение по окружности радиуса
и угловой скоростью
не зависящими, ни от модуля скорости частицы, ни от ее направления.
Проекция магнитной силы на ось Oz равна нулю, поэтому проекция скорости на эту остается постоянной. Следовательно, эта координата изменяется по линейному закону
z = z_0 + \upsilon_1 t = z_0 + \upsilon_0 t \cos \alpha\) . (6)
Таким образом, движение частицы можно представить в виде суперпозиции равномерного движения вдоль оси Oz и равномерного движения по окружности в перпендикулярной плоскости. Траекторией этого движения является винтовая линия, радиус которой определяется формулой (3), а шаг рассчитывается по формуле
h = \upsilon_1 t = 2 \pi \frac\cos \alpha\) . (7)
Таким образом, заряженные частицы движутся по спиралям (точнее винтовым линиям), навивающимся на силовые линии магнитного поля. Такой же характер движения сохраняется и в неоднородном магнитном поле – частицы движутся по спиралям, навивающимся на силовые линии поля, при этом радиус и шаг спирали плавно изменяются с изменением индукции поля. Направление смещения (дрейфа) частиц в магнитном поле определяется направлением начальной скорости частиц и не зависит ни от знака заряда частицы, ни от направления вектора индукции поля, последние определяют только направление вращения вокруг силовой линии. Такое движение заряженных частиц позволяет конструировать различные «магнитные ловушки» для накопления заряженных частиц, управлять движением сильно ионизованного газа (плазмы). Аналогичный характер имеет движение заряженных частиц и в магнитном поле Земли.
Источник
Винтовая линия и винтовые поверхности
Винтовая линия (гелиса) — это пространственная кривая, образованная движением точки, совершающей одновременно поступательное и вращательное движение.
Рассмотрим цилиндрическую винтовую линию (рис. 1) и построим две ее проекции.
Для этого используем две проекции цилиндра, каждую из которых делим на двенадцать равных частей. При перемещении точки из первого положения во второе ее горизонтальная проекция перемещается по окружности на одну двенадцатую часть, а фронтальная — вверх на одну двенадцатую.
Совершая полный оборот, точка в пространстве опишет винтовую линию. Высота, на которую поднимается точка по прямой за полный оборот, называется шагом винтовой линии. Если ось винтовой линии перпендикулярна горизонтальной плоскости проекций, то горизонтальная проекция винтовой линии есть окружность, а фронтальная — синусоида.
На одной поверхности цилиндра может быть несколько винтовых линий.
Винтовые поверхности
Винтовой поверхностью называется поверхность, образованная при перемещении какой-либо линии (образующей) по винтовой линии (направляющей).
Если образующей винтовой поверхности является прямая линия, то поверхность называется линейчатой винтовой поверхностью или геликоидом (от франц. helic — спираль, винтовая линия). Геликоид называется прямым или наклонным в зависимости от того, перпендикулярна образующая оси геликоида или наклонна.
Рассмотрим некоторые виды линейчатых винтовых поверхностей.
- Прямой геликоид образуется движением прямолинейной образующей I по двум направляющим. Одна из направляющих является цилиндрической винтовой линией т, а другая — ее осью Причем во всех своих положениях образующая I параллельна плоскости, которая называется плоскостью параллелизма, перпендикулярной оси II (рис. 2). У прямого геликоида образующая I пересекает ось II под прямым углом.
- Наклонный геликоид отличается от прямого геликоида тем, что его образующая I пересекает ось геликоида под постоянным углом а, не равным прямому углу. Во всех своих положениях образующая I параллельна образующим некоторого конуса вращения. У этого конуса угол между образующей и осью, параллельной оси геликоида, равен ф. Он называется направляющим конусом наклонного геликоида (рис. 3).
Его направляющими являются цилиндрическая винтовая линия т и ее ось II. Образующие геликоида параллельны соответствующим образующим направляющего конуса.
Если образующие геликоида пересекают его ось, то геликоид называется закрытым, если нет — открытым.
Открытый геликоид образуется при винтовом движении прямолинейной образующей I, касающейся во всех свих положениях поверхности малого цилиндра и параллельно плоскости параллелизма, проведенной перпендикулярно оси геликоида (рис. 4).
Источник